Python random.gauss() 方法_Python 菜鸟教程

Python 中的 random.gauss（） 方法生成遵循高斯分布（也称为正态分布）的随机数。它是一系列连续概率分布，取决于两个参数 mu 和 sigma 的值。其中，mu 是平均值，sigma 是高斯分布的标准差。这种分布通常用于统计、数据分析和各种科学领域，包括自然科学和社会科学。

此方法比 random.normalvariate（）方法更快地从高斯（正态）分布生成随机数。

语法

以下是 Python random.gauss（）方法的语法 -

 random.gauss(mu, sigma)

参数

此方法接受以下参数 -

mu：这是高斯分布的平均值。它定义数据点分布所围绕的分布中心。
sigma：这是高斯分布的标准差。它确定分布的分布;标准差越大，分布越宽。

返回值

此方法返回一个遵循高斯分布的随机数。

示例 1

让我们看一个使用 Python random.gauss（）方法从均值为 0、标准差为 1 的高斯分布中生成随机数的基本示例。

import random

# mean
mu = 0 	
# standard deviation
sigma = 1 	

# Generate a Gaussian-distributed random number
random_number = random.gauss(mu, sigma)

# Print the output
print("Generated random number from Gaussian-distribution:",random_number)

以下是输出 -

Generated random number from Gaussian-distribution: 0.9122883847626587

注意：由于其随机性，每次运行程序时生成的输出都会有所不同。

示例 2

此示例使用 random.gauss（）方法生成一个包含 10 个随机数的列表，该列表遵循高斯分布。

import random

# mean
mu = -2	

# standard deviation
sigma = 0.5 	

result = []
# Generate a list of random numbers from the Gaussian distribution
for i in range(10):
	 	 result.append(random.gauss(mu, sigma))

print("List of random numbers from Gaussian distribution:", result)

在执行上述代码时，您将获得如下所示的类似输出 -

List of random numbers from Gaussian distribution: [-1.6883491787714924, -2.2670950449189835, -1.68497316636885, -2.62956757323328, -1.8888429377204585, -2.6139116413700765, -2.287545626016553, -1.5470101615690448, -2.259090829777413, -1.9380772732164955]

示例 3

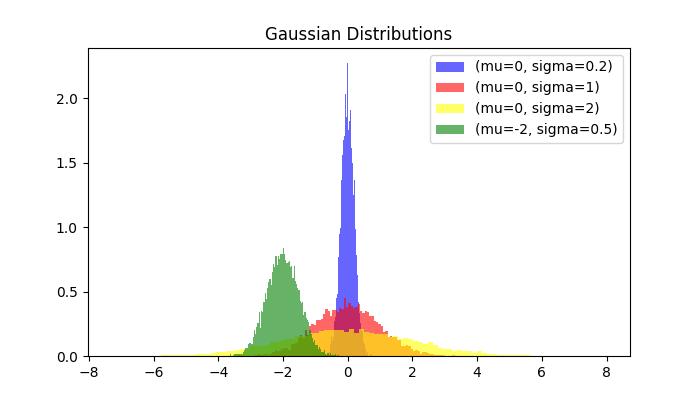
这是另一个使用 random.gauss（）方法的示例，它演示了更改平均值和标准差如何影响高斯分布的形状。

import random
import matplotlib.pyplot as plt

# Define a function to generate and plot data for a given mu and sigma
def plot_gaussian(mu, sigma, label, color):

	 	 # Generate Gaussian-distributed data
	 	 data = [random.gauss(mu, sigma) for _ in range(10000)]

	 	 # Plot histogram of the generated data
	 	 plt.hist(data, bins=100, density=True, alpha=0.6, color=color, label=f'(mu={mu}, sigma={sigma})')

fig = plt.figure(figsize=(7, 4))

# Plotting for each set of parameters
plot_gaussian(0, 0.2, '0, 0.2', 'blue')
plot_gaussian(0, 1, '0, 1', 'red')
plot_gaussian(0, 2, '0, 2', 'yellow')
plot_gaussian(-2, 0.5, '-2, 0.5', 'green')

# Adding labels and title
plt.title('Gaussian Distributions')
plt.legend()

# Show plot
plt.show()

上述代码的输出如下 -

<< Python random.gammavariate() 方法 Python random.lognormvariate() 方法 >>