Python - 递归

递归是一个基本的编程概念，其中函数调用自身以解决问题。这种技术将复杂问题分解为更小、更易于管理的相同类型的子问题。在 Python 中，递归是通过定义一个函数来实现的，该函数在其自己的主体中对自身进行一次或多次调用。

递归的组件

正如我们之前讨论的，递归是一种函数调用自身的技术。在这里，要理解递归，需要了解它的关键组件。以下是递归的主要组件 -

• 基本情况
• 递归大小写

基本情况

Base case 是递归中的一个基本概念，如果作为递归函数停止调用自身的条件。它对于防止无限递归和后续的堆栈溢出错误至关重要。

基本情况为问题的最简单实例提供了直接解决方案，确保每个递归调用都更接近此终止条件。

递归最流行的示例是阶乘计算。在数学上，阶乘定义为 -

 n! = n × (n-1)!

可以看出，我们使用 factorial 本身来定义 factorial。因此，这是编写递归函数的合适情况。让我们扩展上面的定义来计算 5 的阶乘值。

5! = 5 × 4!
	 	5 × 4 × 3!
	 	5 × 4 × 3 × 2!
	 	5 × 4 × 3 × 2 × 1!
	 	5 × 4 × 3 × 2 × 1
= 120

虽然我们可以使用循环来执行此计算，但其递归函数涉及通过递减数字直到达到 1 来连续调用它。

以下示例显示了如何使用递归函数来计算阶乘 -

def factorial(n):

	 	if n == 1:
	 	 	 print (n)
	 	 	 return 1 #base case
	 	else:
	 	 	 print (n,'*', end=' ')
	 	 	 return n * factorial(n-1) #Recursive case
	 	 		
print ('factorial of 5=', factorial(5))

上述程序生成以下输出 -

递归大小写

递归情况是递归函数的一部分，其中函数调用自身以解决同一问题的较小或更简单的实例。这种机制允许将复杂问题分解为更易于管理的子问题，其中每个子问题都是原始问题的较小版本。

递归情况对于向基本情况发展至关重要，确保递归最终终止。

以下是 Recursive 案例的示例。在此示例中，我们将生成斐波那契数列，其中递归情况对前两个斐波那契数列的结果求和 -

def fibonacci(n):
	 	 if n <= 0:
	 	 	 	 return 0 	# Base case for n = 0
	 	 elif n == 1:
	 	 	 	 return 1 	# Base case for n = 1
	 	 else:
	 	 	 	 return fibonacci(n - 1) + fibonacci(n - 2) 	# Recursive case
	 	 	 		
fib_series = [fibonacci(i) for i in range(6)]
print(fib_series)

上述程序生成以下输出 -

使用递归进行二叉搜索

二叉搜索是一种强大的算法，用于在排序列表中快速查找元素，对数时间复杂度使其非常高效。

让我们看另一个例子来了解递归是如何工作的。手头的问题是检查列表中是否存在给定的数字。

虽然我们可以使用 for 循环对列表中的某个数字执行顺序搜索并比较每个数字，但顺序搜索效率不高，尤其是在列表太大的情况下。检查索引 'high' 是否大于索引 'low' 的二叉搜索算法。根据 'mid' 变量中存在的值，再次调用该函数以搜索该元素。

我们有一个数字列表，按升序排列。我们找到列表的中点，并根据所需数字是小于还是大于中点的数字，将检查限制在中点的左侧或右侧。

下图显示了二分搜索的工作原理 -

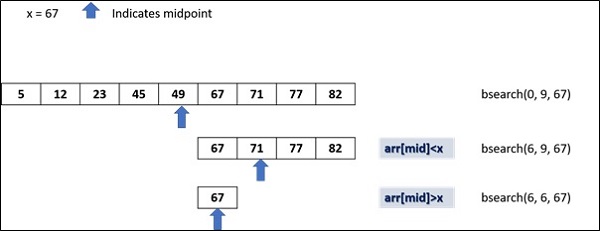
例

以下代码实现了递归二进制搜索技术 -

def bsearch(my_list, low, high, elem):
	 	if high >= low:
	 	 	 mid = (high + low) // 2
	 	 	 if my_list[mid] == elem:
	 	 	 	 	return mid
	 	 	 elif my_list[mid] > elem:
	 	 	 	 	return bsearch(my_list, low, mid - 1, elem)
	 	 	 else:
	 	 	 	 	return bsearch(my_list, mid + 1, high, elem)
	 	else:
	 	 	 return -1

my_list = [5,12,23, 45, 49, 67, 71, 77, 82]
num = 67
print("The list is")
print(my_list)
print ("Check for number:", num)
my_result = bsearch(my_list,0,len(my_list)-1,num)

if my_result != -1:
	 	print("Element found at index ", str(my_result))
else:
	 	print("Element not found!")

输出