Python - 分治算法

---

---

在分治算法的方法中，手头的问题被分成更小的子问题，然后每个问题都独立解决。当我们不断将子问题划分为更小的子问题时，我们最终可能会达到一个不可能再划分的阶段。那些“原子”最小可能的子问题（分数）被解决。所有子问题的解最终合并，以获得原始问题的解。

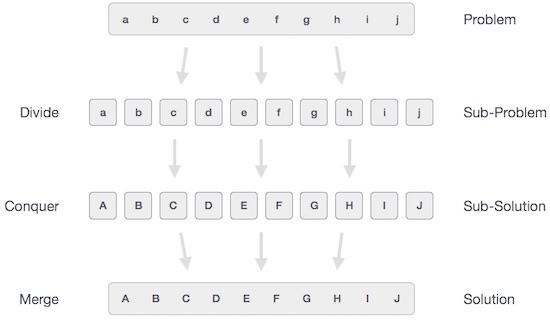
从广义上讲，我们可以将分治算法的方法理解为三个步骤。

分/断

此步骤涉及将问题分解为更小的子问题。子问题应代表原始问题的一部分。此步骤通常采用递归方法对问题进行划分，直到没有子问题进一步可整除。在这个阶段，子问题本质上是原子的，但仍然代表实际问题的一部分。

征服/解决

这一步收到了很多需要解决的小子问题。通常，在这个级别，问题被认为是自行“解决”的。

合并/混合

当较小的子问题得到解决时，这个阶段递归地将它们组合起来，直到它们形成原始问题的解决方案。这种算法方法递归工作并征服 /合并步骤的效果非常紧密，以至于它们看起来是一个。

例子

以下程序是分而治之的编程方法的示例，其中二进制搜索是使用 python 实现的。

二叉搜索实现

在二叉搜索中，我们获取一个排序的元素列表，并开始在列表中间查找一个元素。如果搜索值与列表中的中间值匹配，我们将完成搜索。否则，我们将根据搜索项的值选择是使用列表的右半部分还是左半部分来消除元素列表的一半。

这是可能的，因为列表是排序的，并且比线性搜索快得多。在这里，我们将给定的列表划分并通过选择列表的适当一半来征服。我们重复这个 approcah，直到我们找到该元素或得出它在列表中不存在的结论。

例

def bsearch(list, val):
	 	list_size = len(list) - 1
	 	idx0 = 0
	 	idxn = list_size
# Find the middle most value
	 	while idx0 <= idxn:
	 	 	 midval = (idx0 + idxn)// 2
	 	 	 if list[midval] == val:
	 	 	 	 	return midval
# Compare the value the middle most value
	 	if val > list[midval]:
	 	 	 idx0 = midval + 1
	 	else:
	 	 	 idxn = midval - 1
	 	if idx0 > idxn:
	 	 	 return None
# Initialize the sorted list
list = [2,7,19,34,53,72]

# Print the search result
print(bsearch(list,72))
print(bsearch(list,11))

输出

执行上述代码时，它会产生以下结果 -