必须分析算法的效率和准确性以进行比较,并为某些场景选择特定的算法。进行此分析的过程称为渐近分析。它是指以数学计算单位计算任何操作的运行时间。
例如,一个操作的运行时间计算为 f(n),而另一个操作的运行时间可能计算为 g(n2)。这意味着第一个操作的运行时间将随着 n 的增加而线性增加,而当 n 增加时,第二个操作的运行时间将呈指数增加。同样,如果 n 非常小,则两个操作的运行时间将几乎相同。
通常,算法所需的时间分为三种类型 -
- 最佳情况 - 程序执行所需的最短时间。
- 平均大小写 - 程序执行所需的平均时间。
- 最坏情况 - 程序执行所需的最长时间。
渐近符号
常用的渐近表示法,用于计算算法的运行时复杂度。
- ο 表示法
- Ω表示法
- θ 表示法
Big Oh 表示法,Ο
表示法 Ο(n) 是表示算法运行时间上限的正式方式。它衡量最坏情况下的时间复杂度或算法可能完成的最长时间。
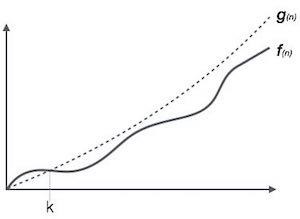
例如,对于函数 f(n)
Ο(f(n)) = { g(n) : there exists c > 0 and n0 such that f(n) ≤ c.g(n) for all n > n0. }
Omega 表示法,Ω
表示法 Ω(n) 是表示算法运行时间下限的正式方式。它衡量最佳案例时间复杂度或算法可能完成的最佳时间。
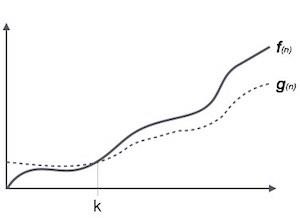
例如,对于函数 f(n)
Ω(f(n)) ≥ { g(n) : there exists c > 0 and n0 such that g(n) ≤ c.f(n) for all n > n0. }
Theta 表示法,θ
表示法 θ(n) 是表示算法运行时间的下限和上限的正式方式。它表示如下 -
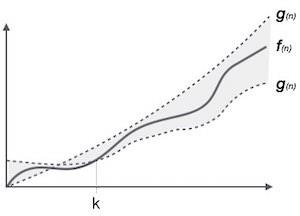
θ(f(n)) = { g(n) if and only if g(n) = Ο(f(n)) and g(n) = Ω(f(n)) for all n > n0. }
常见的渐近符号
下面提到了一些常见的渐近符号列表 -
| constant | − | Ο(1) |
| logarithmic | − | Ο(log n) |
| linear | − | Ο(n) |
| n log n | − | Ο(n log n) |
| quadratic | − | Ο(n2) |
| cubic | − | Ο(n3) |
| polynomial | − | nΟ(1) |
| exponential | − | 2Ο(n) |



